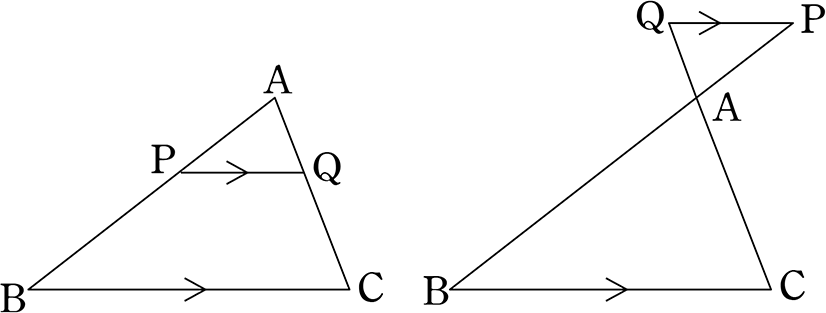
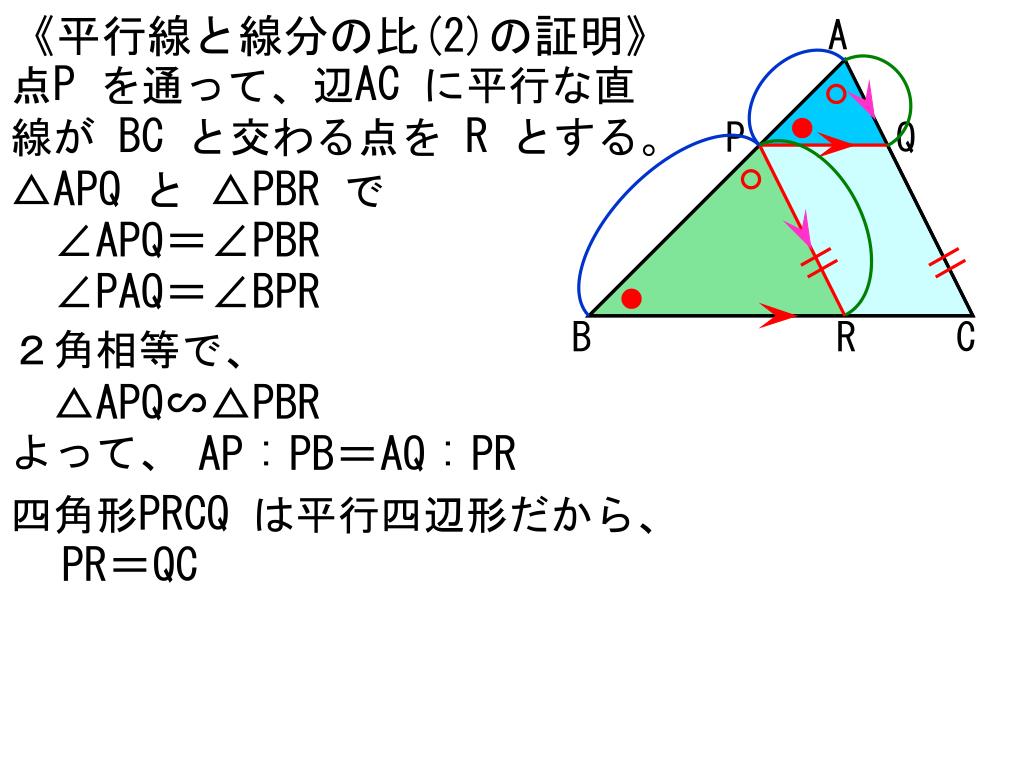
平行線で区切られた線分の比の定理 「平行線と比の定理」の 型と 型は、台形のようなものにも応用できますね! 直線 t を平行移動させた t' も、 当然 a':b' ですね! (t と t' の間の空間は平行四辺形) 実は、3本の平行線(に交わる直線の「 比 」は線分ABを3:2の比に内分する点を作図するときを説明しましょう。まず,AC:CD=3:2 となる点C,dを作図するところまではいいですね。次に, 点Cを通り線分BDに平行な直線を作図してみます。 このとき,平行四辺形BDCQを作図することを考えるとわかりやすいですよ。つまり,CD=QB,BD=QCとなる 平行線と線分の比の定理のひとつに、 PQ//BC⇒AP/AB=PQ/BC がありますが、 この逆、つまり AP/AB=PQ/BC⇒PQ//BC が成り立たないことを示す判例を教えてください。 下図のようなこともあるということでしょうか?
3
平行線と線分の比 平行四辺形
平行線と線分の比 平行四辺形-右図の平行四辺形 においabcd て, の中点をE, と の交ad ec bd 点をFとするとき と , fde fbc 問題番号問いの面積の比を求めなさい。 12 正解 1:4 誤 答 例 つまずき原因 分析と解消 1 無解答 2つの三角形が相似であることに気が付かな30ページ い。 12-1三角形の1つの 辺に平行な直線 を引き、そこに できる線分の比 について長さを 調べ、それを証 明する。 平行線と線分の 比についての性質 に関心をもち、平 行線の性質を三角 形の相似条件を用 いて証明しようと している。〔観察・ ノート〕 平行線と線分の 比についての性質



平行四辺形の性質1
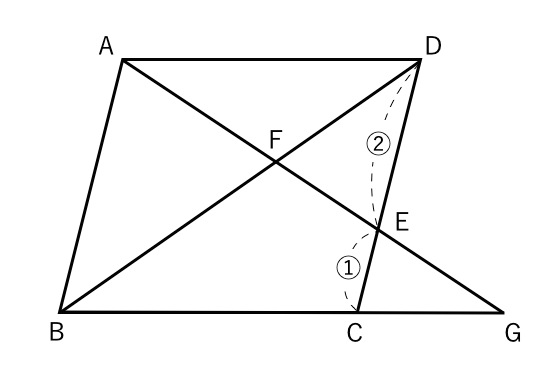
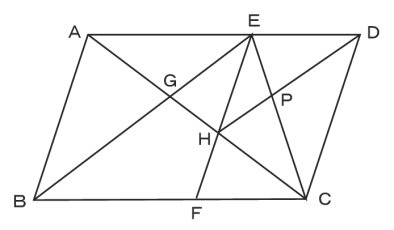
こんにちは。今回は神奈川県の入試問題より, 平行線と線分の比に関する問題です。それではどうぞ。 図において, 四角形abcdは平行四辺形である。また, 点eは線分bc上の点であり, 三角形abeは正三角形である。さらに, 線分abの中点をfとし, 線分aeと線分cfとの交点をgとする。平行線と台形中3数学 問題をノーヒントでやってみよう 略解をチェックしよう 攻略ポイントを確認しよう ・平行線で三角形を作り、線分の比を利用する 完璧じゃなかったら授業動画を見よう やる気先生の授業動画 327K subscribers3.平行四辺形 4.特別な平行四辺形,平行線と面積 5.1次関数と図形 Ⅵ 確率 1.場合の数と確率 確率 1~2 2.いろいろな確率の求め方 Ⅶ 四分位数と箱ひげ図 1.四分位数と箱ひげ図の基礎 四分位数と箱ひげ図 1~2 2.四分位数と箱ひげ図の応用 3 pdf zip Ⅰ 式の計算 1.多項式の計算
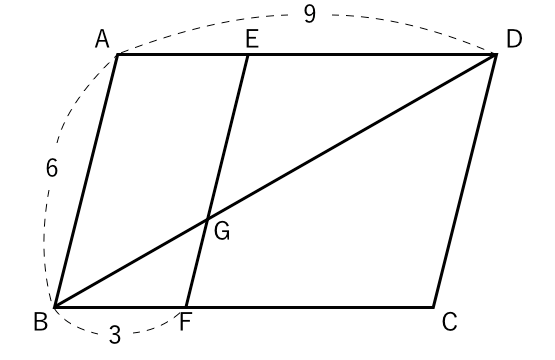
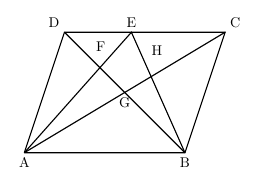
平行線と線分の比の性質を証明するには,三角形と比の定理を用いればよいことに気付 き,証明をすると共に,その性質を用いて線分の長さを求めることができる。 ②コンピュータ活用の意図 ・「直線を移動させる機能」を使って,「三角形と比の定理 平行四辺形と線分比>>中学三年生 平行四辺形ABCDの辺AB,BC上に点P、Qをとり、 AP:PB=2:3、 BQ:QC=1:3 となるようにする。 平行線の線分比の性質を使った問題です。 図形を見てどことどこが相似になりそうかわかるようになると良いですね。 夢を叶える塾 数学を通して夢を叶える力を育む米沢市の学習塾 フォローする 夢を叶える塾 簡単なご案内;
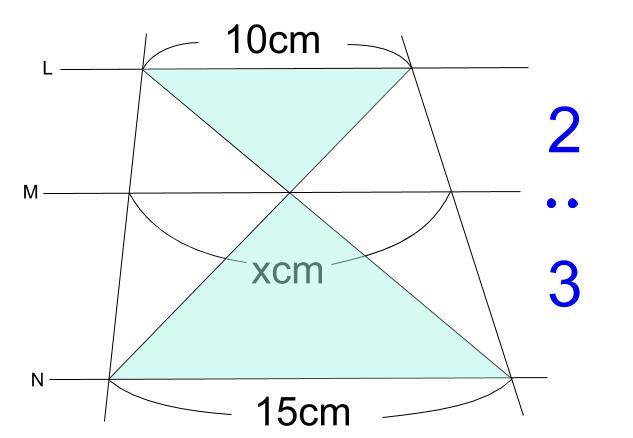
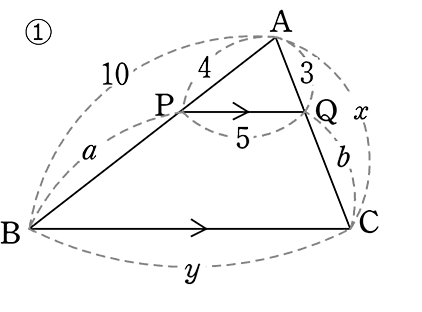
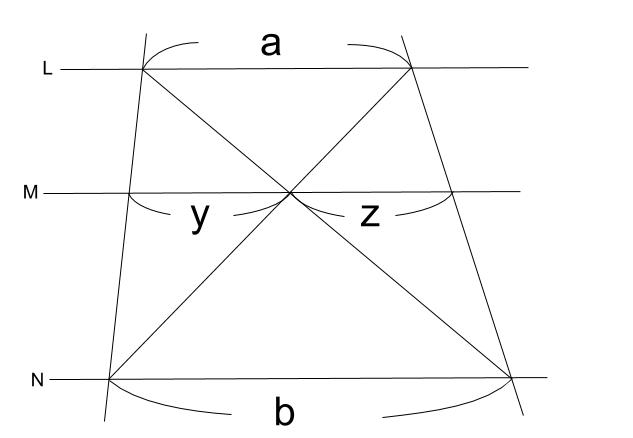
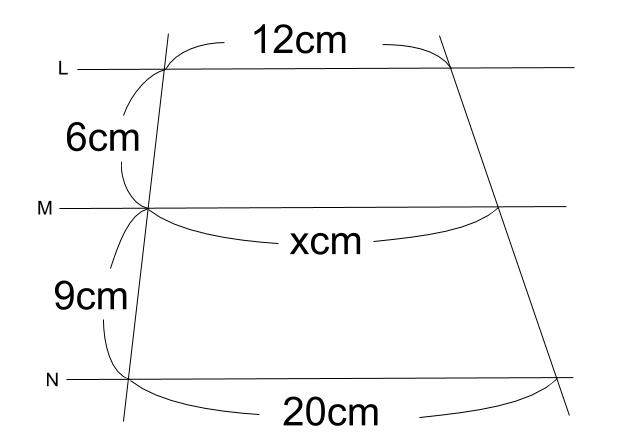
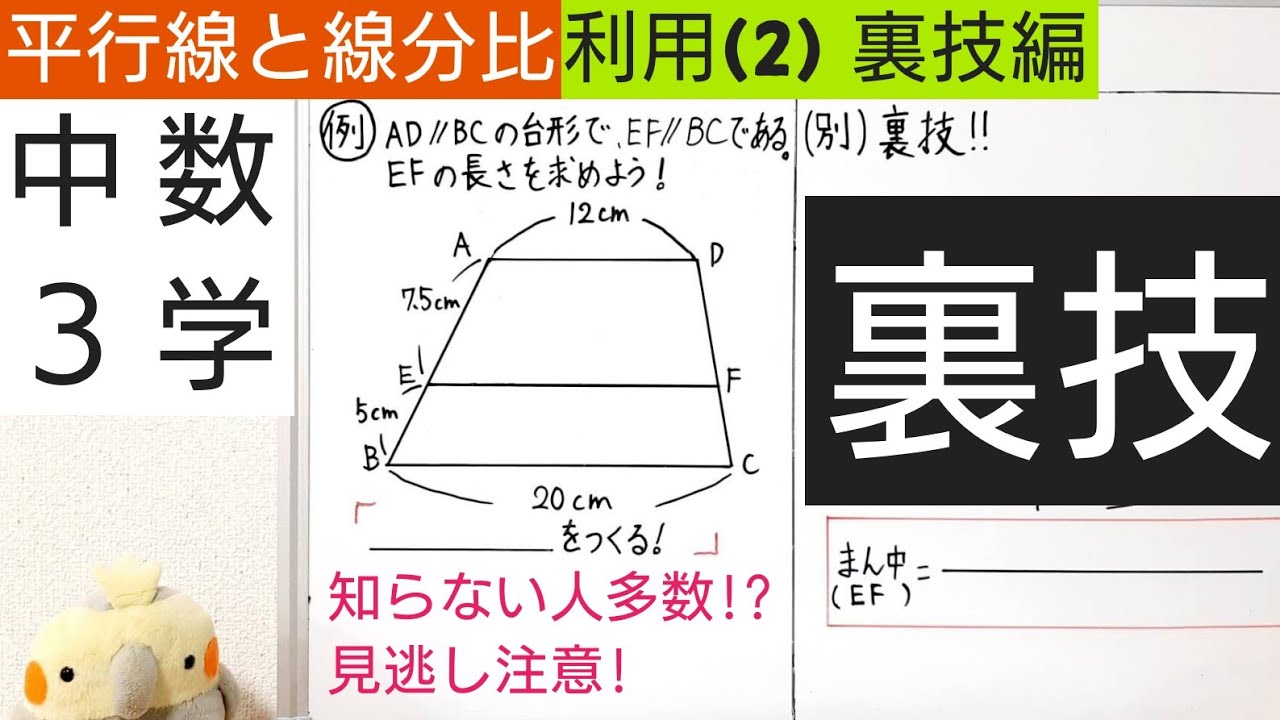
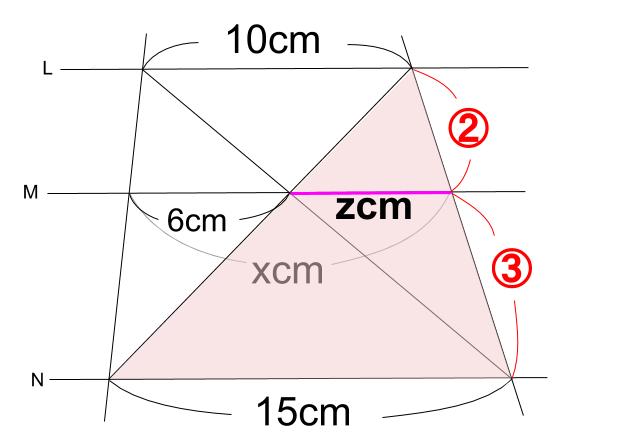
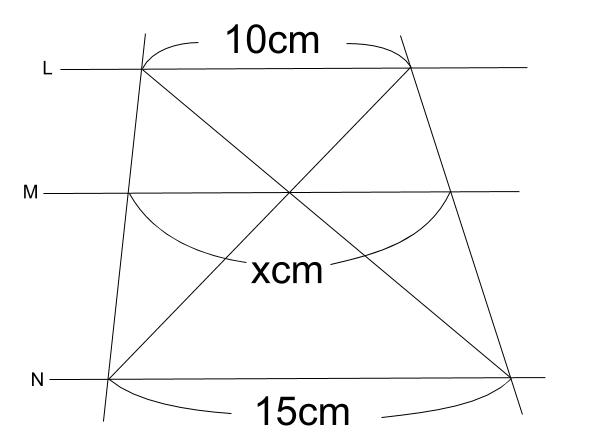
例えば平行四辺形を分割した線分比という受験の定番問題があります。 「線分比を求めるには相似比がもっともシンプルである」 「相似比を求めるには三角形の相似が役立つ」 「相似な三角形は平行線で作るのが分かりやすい」平行線と線分の比の利用平行線と線分の比を用いる問題を練習しましょう。\(2\) つの似ている図の問題を比較して、平行線と線分の比の利用について理解を深めましょう。例題1次の図で、直線 \(L,M,N\) が平行のとき、\(x\) の値を求めなさい。①②解説①と②で似たような図です。もちろんどちら 123 平行線の幾何Ⅱ(三角形と線分比②および内分・外分) 1 理一の数学事始め 21年8月26日 0025 フォローしました これまでも使っているのですが線分の内分点・外分点について説明します。 下の図のように線分ABがあって、線分AB上の点Pは線分をPを




相似 平行四辺形と面積比の問題を徹底解説 数スタ
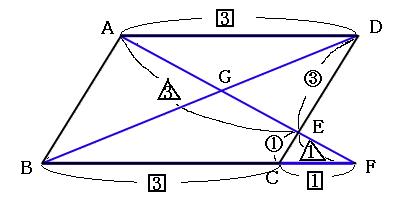



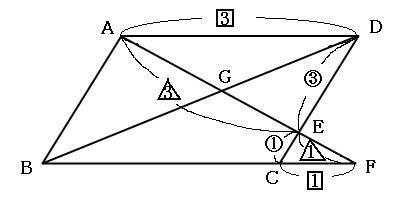
平行四辺形の対角線を3つに分ける問題を解くときはチョウチョを2匹探せ
似 10 「平行線と比」の定理を利用して,線分 課題把握,解決の見通しや確認を行う。 の長さなどを求めることができるようにす る。 の 応 11 三角形の2辺を等しい比に分ける2点を結 べば,その線分は残りの辺に平行となること 用 を考えさせる。=== 平行線と線分の比 === 三角形の相似条件 次の(1)(2)(3)は三角形の相似条件と呼ばれており,そのうち1つでも成り立てば2つの三角形は相似になる. 逆に,2つの三角形が相似であるとき,次の(1)(2)(3)はすべて成り立つ.イ 三角形の相似条件などを基にして図形の基本的な性質を論理的に確かめること。 ウ 平行線と線分の比についての性質を見いだし,それらを確かめること。 エ 基本的な立体の相似の意味と,相似な図形の相似比と面積比及び体積比の関係について理解す



相似な図形 平行線と線分の比 平行四辺形 苦手な数学を簡単に



中学数学 平行線と線分の比 その2 中学数学の無料オンライン学習サイトchu Su
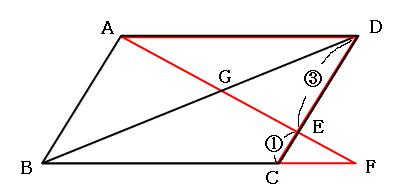
この図は、さっきと同じ図なんじゃが、不要な線などを消したんじゃ 線分XEと線分DGは平行じゃから、平行と線分比の関係から、 AX XD = AE EG が言えるわけじゃな 同じものじゃが、分数の形で書いておくと、 mathjax 図のような平行四辺形abcdがあり、点e、fはそれぞれ辺cd、adの真ん中の点です。このとき、 斜線(しゃせん)部分の面積は平行四辺形の面積の何倍ですか。 (海城中 07年・2回) <問題2の考え方と答え> 次に、斜線の部分の面積を表しやすいように、点g と h をつけておきます。相似比の練習問題(平行四辺形5) 問1図のように、平行四辺形abcd の辺ad 上にae:ed =1:2 となる点e をとり、e から 辺ab に平行な直線を引き、辺bc との交点をf とします。さらに、対角線ac とef



相似な図形 平行線と線分の比 平行四辺形 苦手な数学を簡単に




中3 19 2 平行四辺形と相似 Youtube
円,角,垂直,平行 円と直線 平行四辺形の性質と条件 4章 平行と合同(中2学年) 5 多角形の内角と外角 拡大、縮小 対頂角、平行線の性質と条件 相似な図形、相 図形の性質の調べ方 三角形の合同条件 平行線と線分の比 証明のしくみ 中点連結定理 5章 平面図形(中1数学25章図形の性質と証明「平行線と面積」<応用問題> 組 番 名前 1右の図において,四角形ABCDは平行四辺形です。 このとき, BCFと面積が等しい三角形をすべて 答えなさい。 2右の図のように,平行四辺形ABCDの辺BC上に点E平行線と線分の比の性質を 用いて,線分の長さや比を求 めることができる。 平行線と線分の比の 性質を理解すること ができる。 5 単元計画(8時間) 次 時 学習活動・内容 生徒の思考 指導・援助の手だて 1 (1) 1 平行線と線分の比についての課題を見いだす。



3




中点連結定理とは 逆の証明や平行四辺形の問題もわかりやすく解説 遊ぶ数学
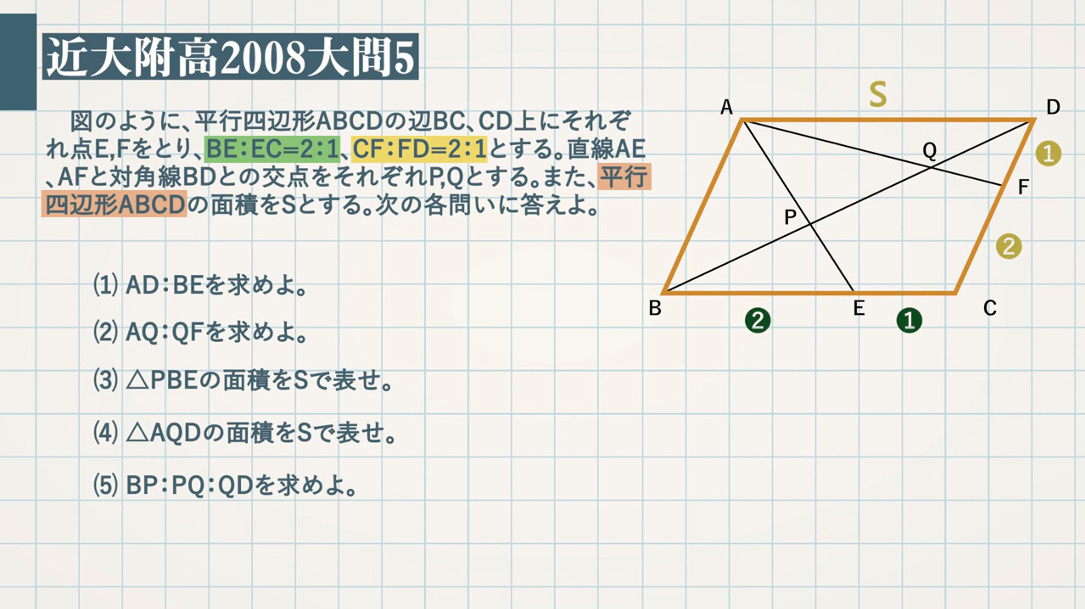
相似と線分比1(平行四辺形) abcdでaeeb=13, bffc=21のとき eggdの線分比を求めよ。 a b c d e f g0:13 図のように、平行四辺形 A B C D の辺 B C 、 C D 上にそれぞれ点 E, F をとり、 B E E C = 2 1 、 C F F D = 2 1 とする。 直線 A E 、 A F と対角線 B D との交点をそれぞれ P, Q とする。 また、平行四辺形 A B C D の面積を S とする。 次の各問いに答えよ。 (1) A D B E を求めよ。 (2) A Q Q F を求めよ。 (3) P B E の面積を S で表せ。 (4) A Q D の面積を S で表せ。右の図のように,平行四辺形 abcd がある。辺 ab の中点を e とし,点 e を通り線分 bd に平行な直線と辺 ad との交点を f とする。また,線分 cf と線分 ed, bd との交点をそれぞれ g, h とする。 このとき,次の(1),(2)の問いに答えなさい。 (1) 略




相似 平行四辺形と面積比の問題を徹底解説 数スタ
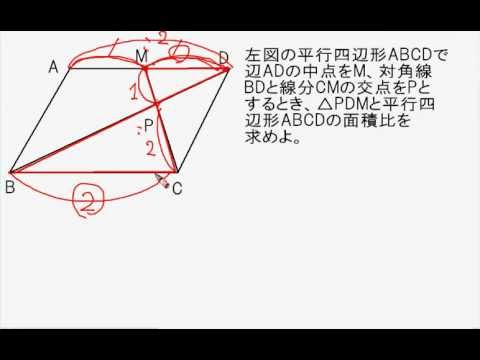



ご質問への解説 平行四辺形面積比 Youtube
よって1組の対辺が平行でその長さが等しいので四角形pqrsは平行四辺形になる。 平行線と比の定理 A B C D E p q r l m F 平行な3つの直線p, q, rが 次の平行四辺形を見てみましょう。 これは、直線 A, D と、直線 a, c を使ってできる平行四辺形です。このように、斜めの線を2つ選び、横の線を2つ選ぶと、それらを使って平行四辺形を作ることができます。逆に、どの平行四辺形も対応する斜めの線2本と横数学35章図形と相似「平行線と線分の比」<準備問題・解答> 1 2組の向かい合う辺がそれぞれ平行な四角形 2 2組の向かい合う角がそれぞれ等しい。 ※順序は問わない。 対角線がそれぞれの中点で交わる。 3!錯角 "DOC #2組の角がそれぞれ等しい
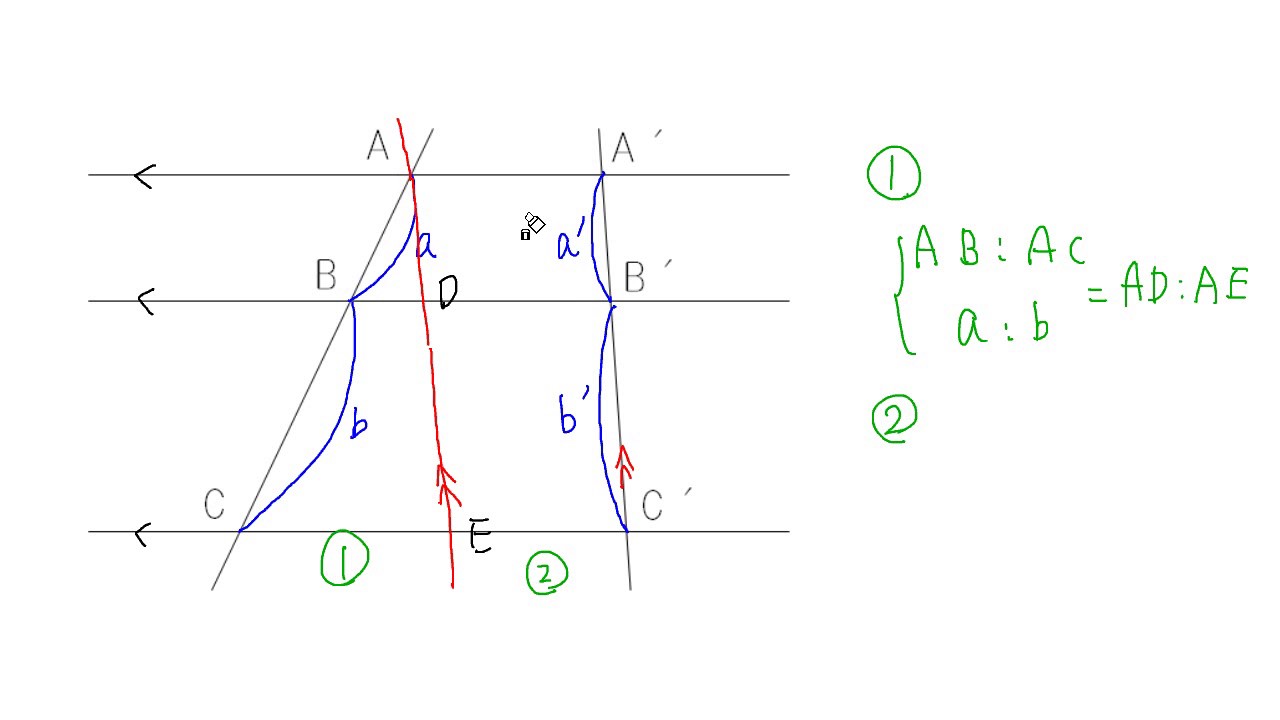



平行線と線分の比 Youtube
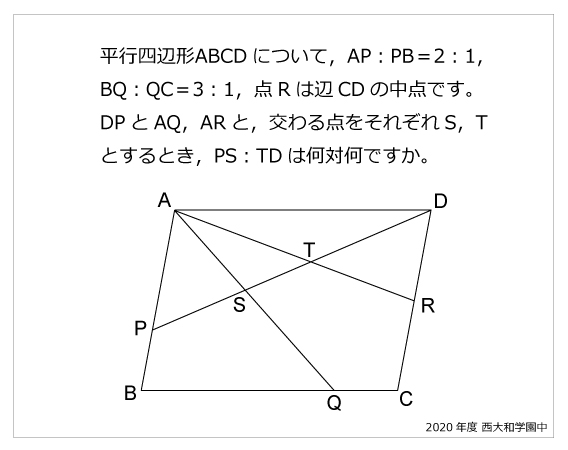



今年の1問 年西大和学園中 平行四辺形と比 算数星人のweb問題集 中学受験算数の問題に挑戦
平行線と線分の比:平行線 /三角形と平行線/平行四辺形と平行線/平行線と相似の証明/ 中点連結定理:長さを求める/ 証明問題など/底辺比と面積比など/相似比と面積比/ 相似比と体積比など /FdData 入試製品版のご案内 FdData 入試ホームページ掲載のpdf ファイル(サンプル)一覧平行線と線分の比 \(2\) つの図形において、いくつかの辺の長さがわかっているとき、長さがわからない辺の長さを求めるために平行線の定義を利用することがあります。 証 明三角形と線分の比/平行線にはさまれた線分の比/平行線と線分比応用/ 三角形の角の二等分線と線分の比 /中点連結定理:証明問題/長さ・角度の計算/全般/ FdData 中間期末製品版のご案内 FdData 中間期末ホームページ 掲載のpdf ファイル(サンプル)一覧 ※次のリンクはShiftキーをおし
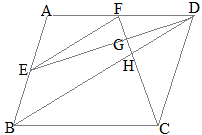



相似図形 高校入試問題




補助線の引き方のコツ 中学受験算数 平面図形
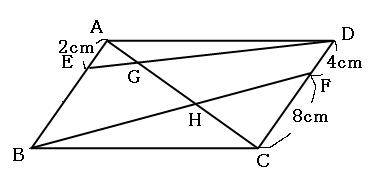
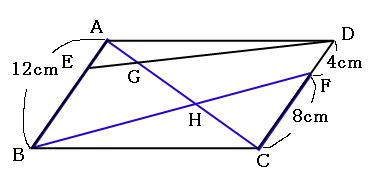
というわけで今回はこの「平行線と線分の比」の平行四辺形の問題について解説していきます。 まずは図に比を書き込む 問題 問 下の図の平行四辺形abcdにおいて、beec=4:3、cffd=2:1である。 (1) aggeを求めなさい。 (2) bgghhdを求めなさい。ち、それを 平行線 の性質 や三角形 の相似条件 をも とに 調べようと する 。 平行線 と線分 の比の性質 を使 って 、いろい ろな 線分 の長さを 求 めることができ る。 いくつかの 平行 線が他の直線 と交 わってできる 線分 の比の性質 を理解 する 。 2 平3 平行線と線分の比 「平行線に直線が交わるとき、その交点の間の比は等しくなる」ことを次のように 証明した。直線l,m,nが平行であるとき、かっこに当てはまる語をうめよう。 点aを通り、直線a′に平行な直線を引き、それと直線m,nの交点をd,eとした。




角の2等分と線分の比 中学数学の無料オンライン学習サイトchu Su
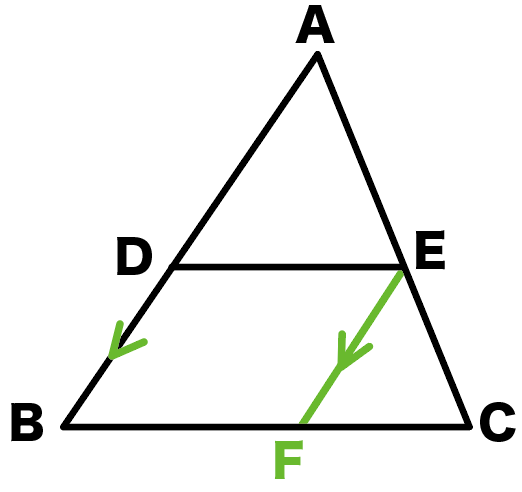



3分でわかる 平行線と線分の比の2つの証明 Qikeru 学びを楽しくわかりやすく



平行四辺形の対角線を3つに分ける問題を解くときはチョウチョを2匹探せ




無料 中3数学 標準問題 解答プリント 328 図形の相似3 線分の比



第5章21 面積の比と体積の比 平方四辺形の相似比と面積比 フロントエンドなブログ



平行四辺形と比 教遊者
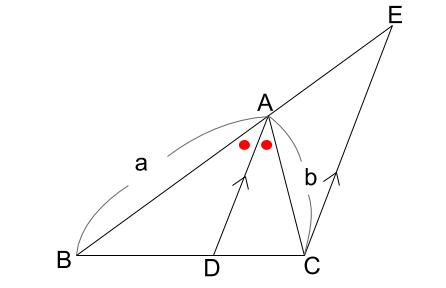



角の2等分と線分の比 中学数学の無料オンライン学習サイトchu Su




中学数学3 平行線と線分の比の証明 中学数学 By となりがトトロ マナペディア
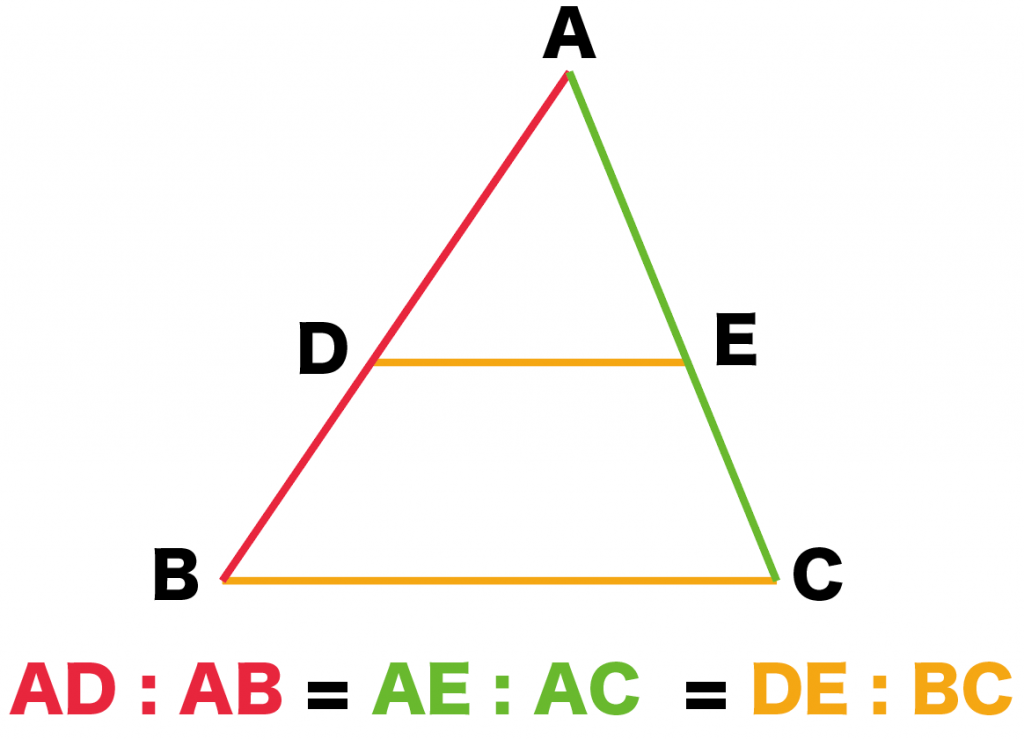



3分でわかる 平行線と線分の比の2つの証明 Qikeru 学びを楽しくわかりやすく



相似5 平行線と線分比 3 デジタル教科書 電子教科書
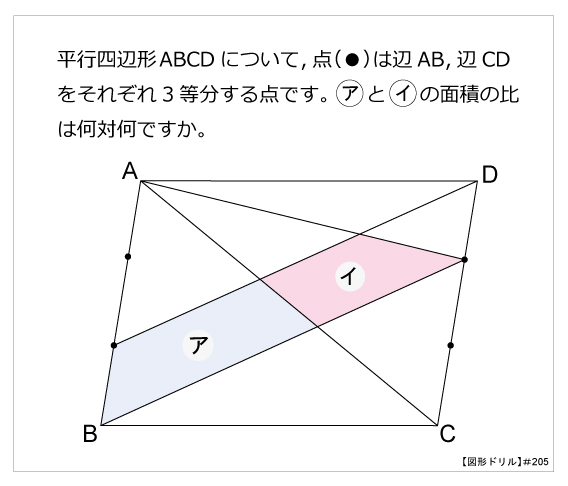



図形ドリル 第5問 平行四辺形内の面積比 算数星人のweb問題集 中学受験算数の問題に挑戦
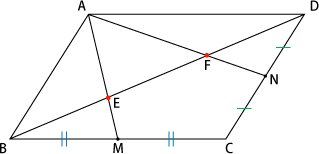



基礎学力アップシート 3年生 平行四辺形の辺の比を考えよう
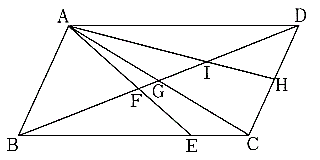



北辰塾 情報局 直撃 中学入試問題 第97回 法政大第二中 相似 平行四辺形の中の三角形
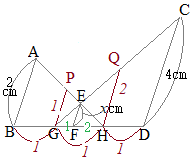



相似図形 高校入試問題




算数図形編 面積比 線分比 相似 面積比を辺の長さで表そう 中学受験 高校受験パスナビ




Ac Be E 5cn Descubre Como Resolverlo En Qanda



次の図の平行四辺形abcdにおいて Ab Efとする このとき Yahoo 知恵袋




高校数学a 三角形の内角 外角の二等分線と辺の比の関係とその証明 受験の月
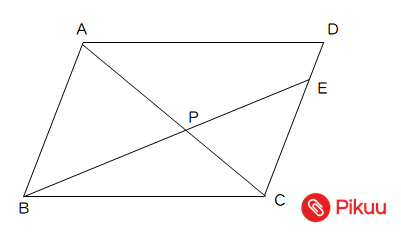



高校入試対策数学 面積比に関する対策問題 Pikuu
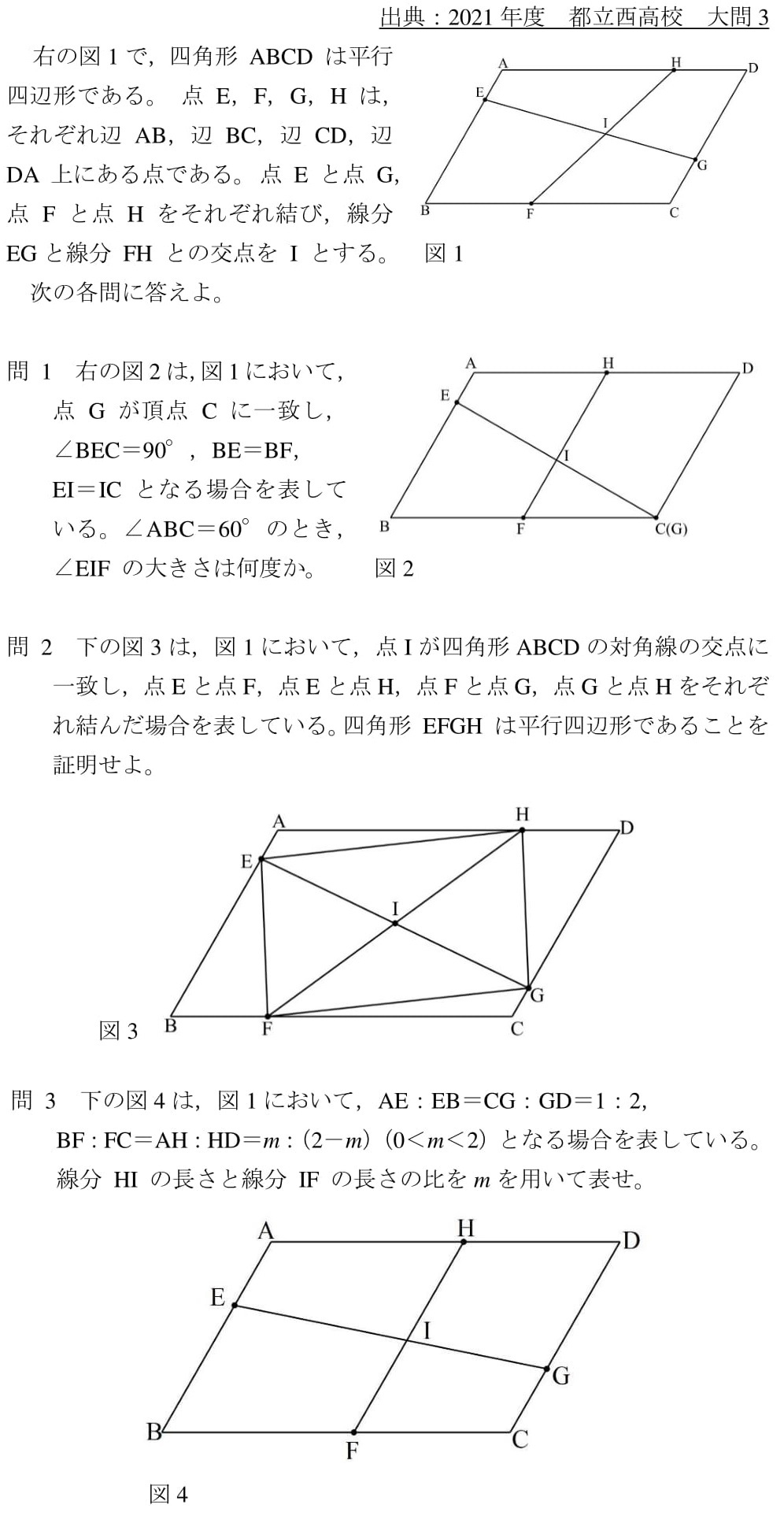



21都立西 平行四辺形の難問証明 高校入試 数学 良問 難問



中学数学 図形の相似




Mathematics 相似 3 平行線と比 みんなが苦手な相似頻出問題 働きアリ




平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




相似な図形 平行線と線分の比 平行四辺形 苦手な数学を簡単に



中学数学 平行線と線分の比 その2 中学数学の無料オンライン学習サイトchu Su



平行四辺形の対角線を3つに分ける問題を解くときはチョウチョを2匹探せ



中学3年の数学 平行線と線分の比の利用 次の四角形abcdは 平行四辺形 Yahoo 知恵袋




中3数学 相似と線分比1 平行四辺形 Youtube



Studydoctor平行線と線分の比の利用 中3数学 Studydoctor




平行四辺形の問題です 平行四辺形abcdがあります 辺abを2 3に分 数学 教えて Goo



中学数学 図形の相似
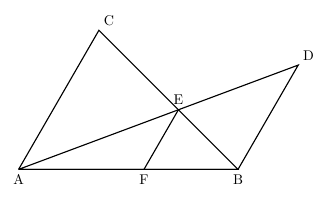



平行線の線分比の問題の解法 夢を叶える塾



Http Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Yaruki Suugaku Documents M3011 Pdf




中3数学 中点連結定理を使う証明 例題編 映像授業のtry It トライイット



平行四辺形の対角線を3つに分ける問題を解くときはチョウチョを2匹探せ




分かるかたお願いします 平行線と線分の比の問題です Clear



中学数学 平行線と線分の比 その2 中学数学の無料オンライン学習サイトchu Su




相似 平行四辺形と面積比の問題を徹底解説 数スタ
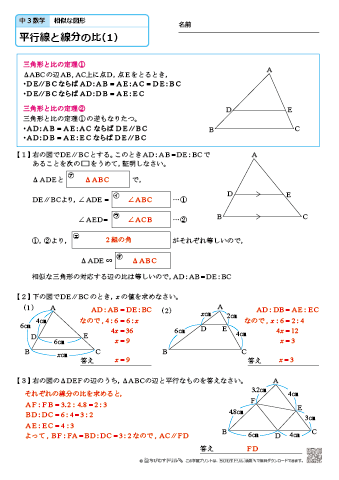



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



Ppt 5 図形と相似 Powerpoint Presentation Free Download Id



中3数学 15 平行線と線分の比の利用 2 裏技 Youtube




Ac Be E 5cn Descubre Como Resolverlo En Qanda



平行四辺形の対角線を3つに分ける問題を解くときはチョウチョを2匹探せ




四角形abcdが平行四辺形 Bfが Abcの二等分線 Abfの面積が6cm のとき Clear



平行線の線分比の問題の解法 夢を叶える塾



中学数学 平行線と線分の比 その2 中学数学の無料オンライン学習サイトchu Su




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学



平行線と線分の比 中学3年 数学クラブ




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学



相似な図形 平行線と線分の比 平行四辺形 苦手な数学を簡単に



中3数学 相似や比の応用問題を解くためのテクニック 個別指導塾のyou 学舎日記 公式ブログ




平行四辺形と線分比 中3数学 図形と相似13 Youtube



相似な図形 平行線と線分の比 平行四辺形 苦手な数学を簡単に
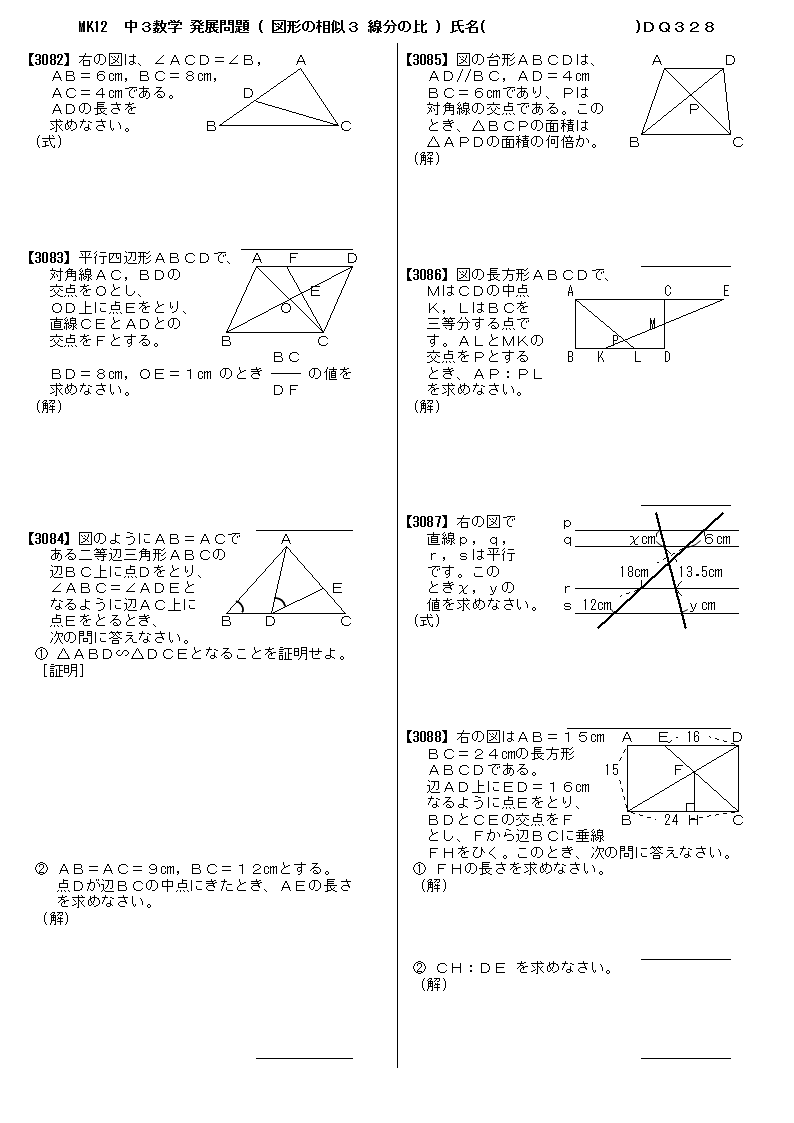



無料 中3数学 発展 応用問題 問題プリント 328 図形の相似3 線分の比



平行四辺形を分ける面積比の求め方 算数解法の極意




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学




Ac Be E 5cn Descubre Como Resolverlo En Qanda



中3数学 相似や比の応用問題を解くためのテクニック 個別指導塾のyou 学舎日記 公式ブログ



中学数学 平行線と線分の比 その2 中学数学の無料オンライン学習サイトchu Su




平行線と線分の比の証明 浅野直樹の学習日記



対角線の長さ 本数の求め方とは 公式を使って一瞬で計算しよう Studyplus スタディプラス



ややこしや 線分の比 と 面積の比 名寄 算数数学教室より
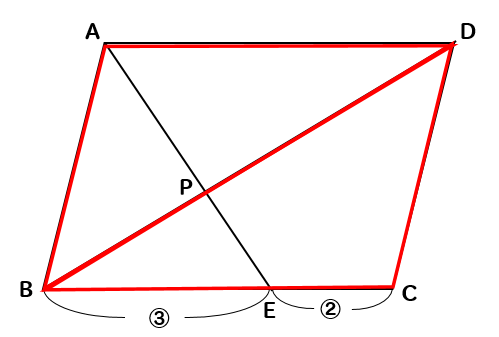



相似 平行四辺形と面積比の問題を徹底解説 数スタ



1



1
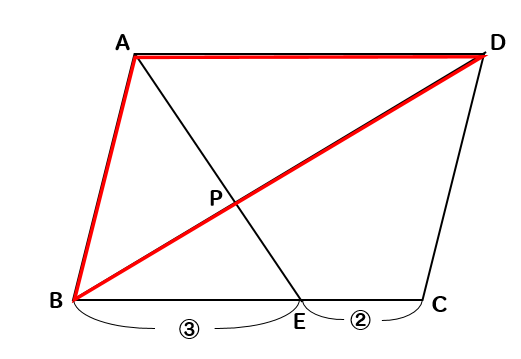



相似 平行四辺形と面積比の問題を徹底解説 数スタ
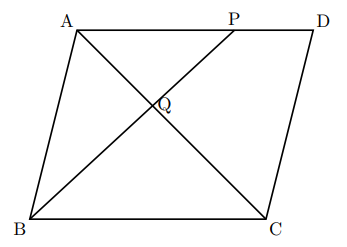



攻略法 平行四辺形と面積 数樂管理人のブログ
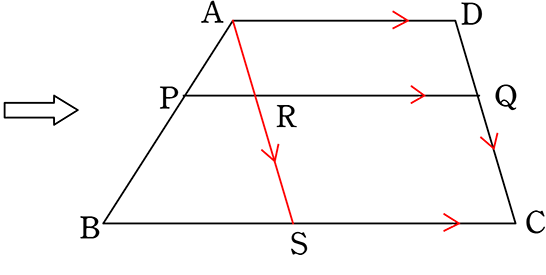



中学数学 図形の相似
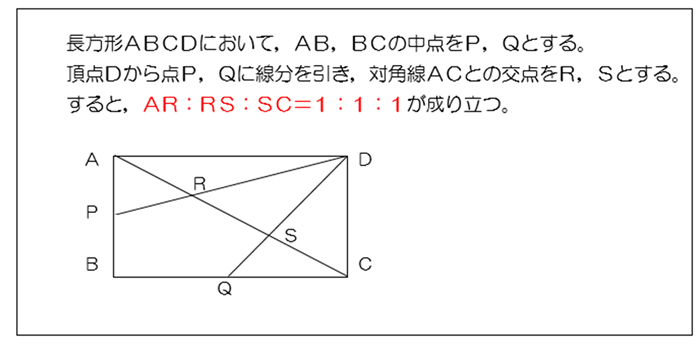



授業実践記録 数学 新しい 定理 とその活用 啓林館
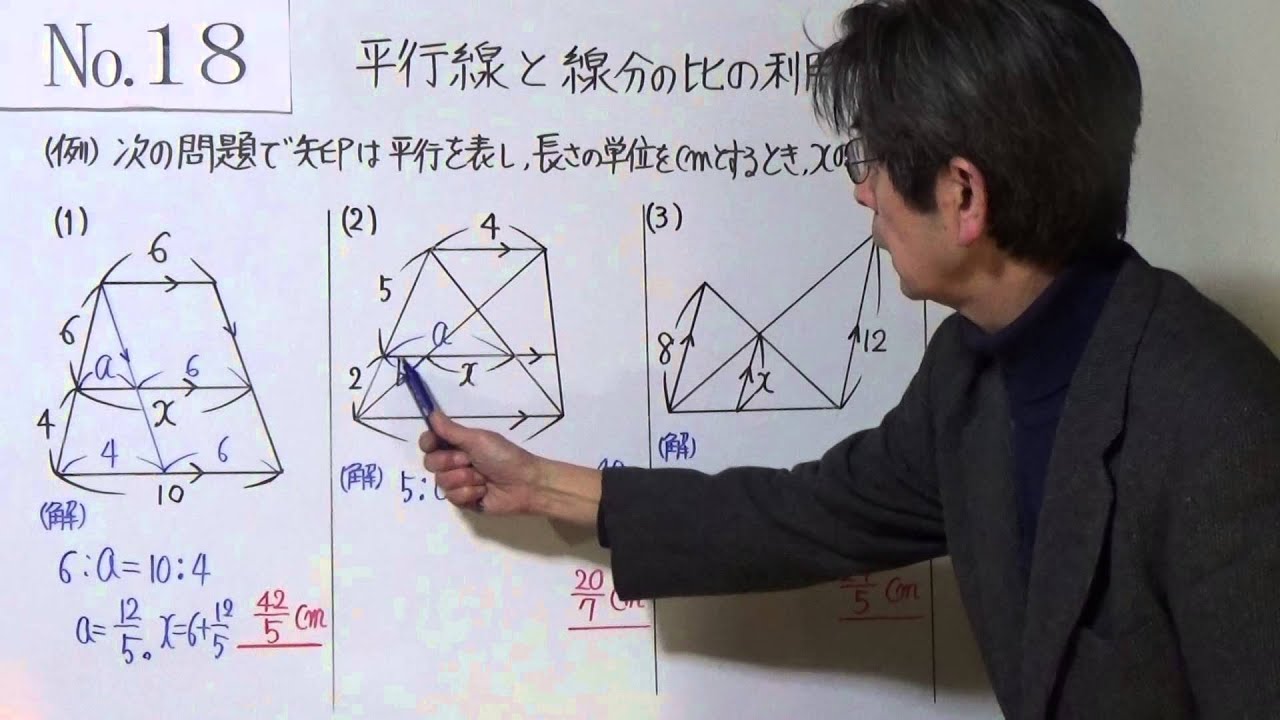



中3 18 5 平行線と線分の比の応用 Youtube
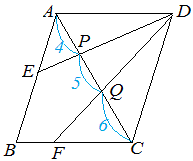



面積比




高校入試 平行四辺形と線分の比 Youtube



平行四辺形と比 教遊者




中3数学 図形と相似23 平行線と線分の比 比の合成 連比 すべて無料 星組の中学数学講座



平行性変形でのベクトルの小手技
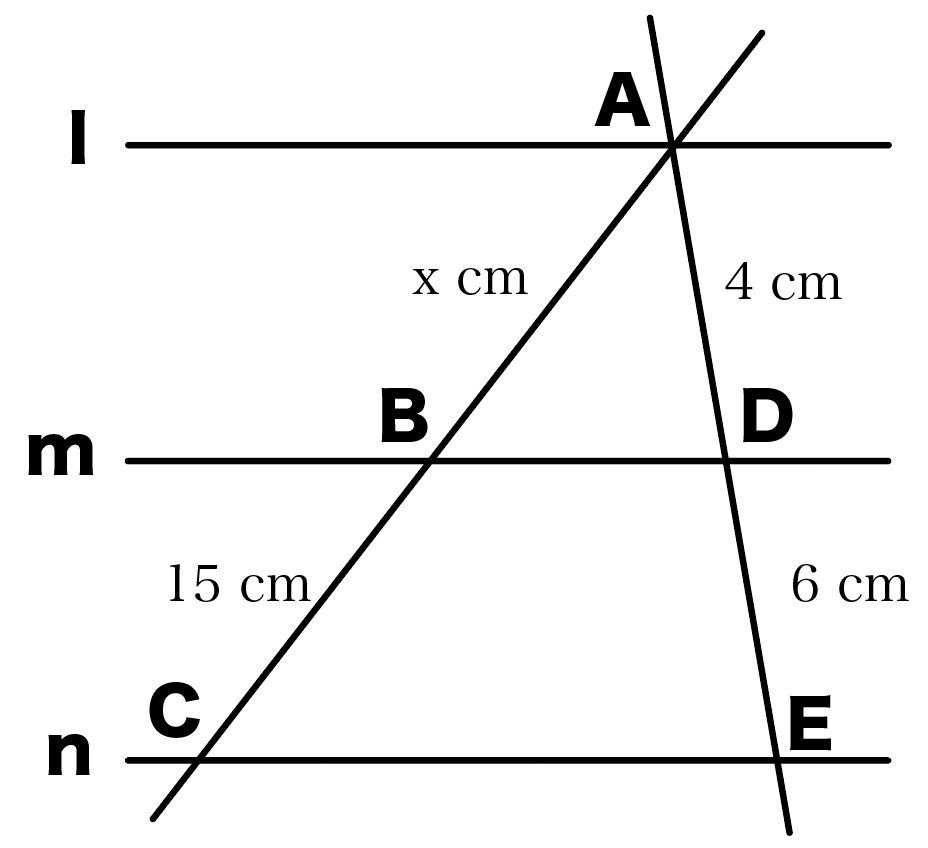



平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




平行線と線分の比 三角形の比の取り方を簡単な問題で覚えよう 中学や高校の数学の計算問題




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学
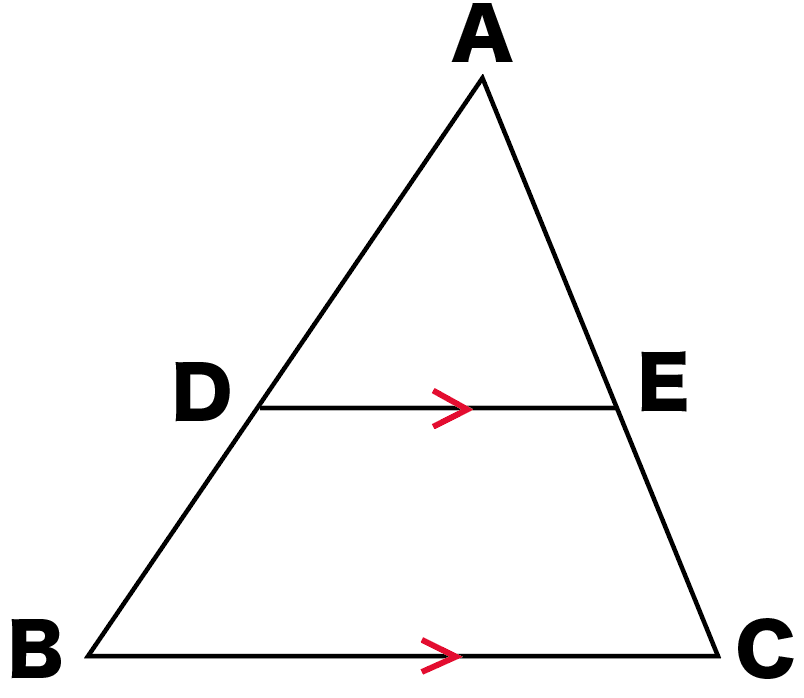



3分でわかる 平行線と線分の比の2つの証明 Qikeru 学びを楽しくわかりやすく



高校入試 英語 数学 図形と相似 平行線と線分の比




Abcd 1 ce31 2 Bee Descubre Como Resolverlo En Qanda




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学
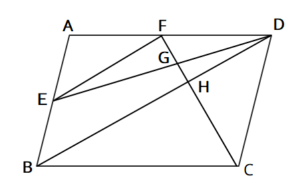



高校入試数学 連比の対策問題 中学生勉強サイトあかね先生



平行四辺形の性質1



図形問題が驚くほど得意になる基本問題とは あおぞら塾




中2 相似 平行線と線分の比 中学生 数学のノート Clear
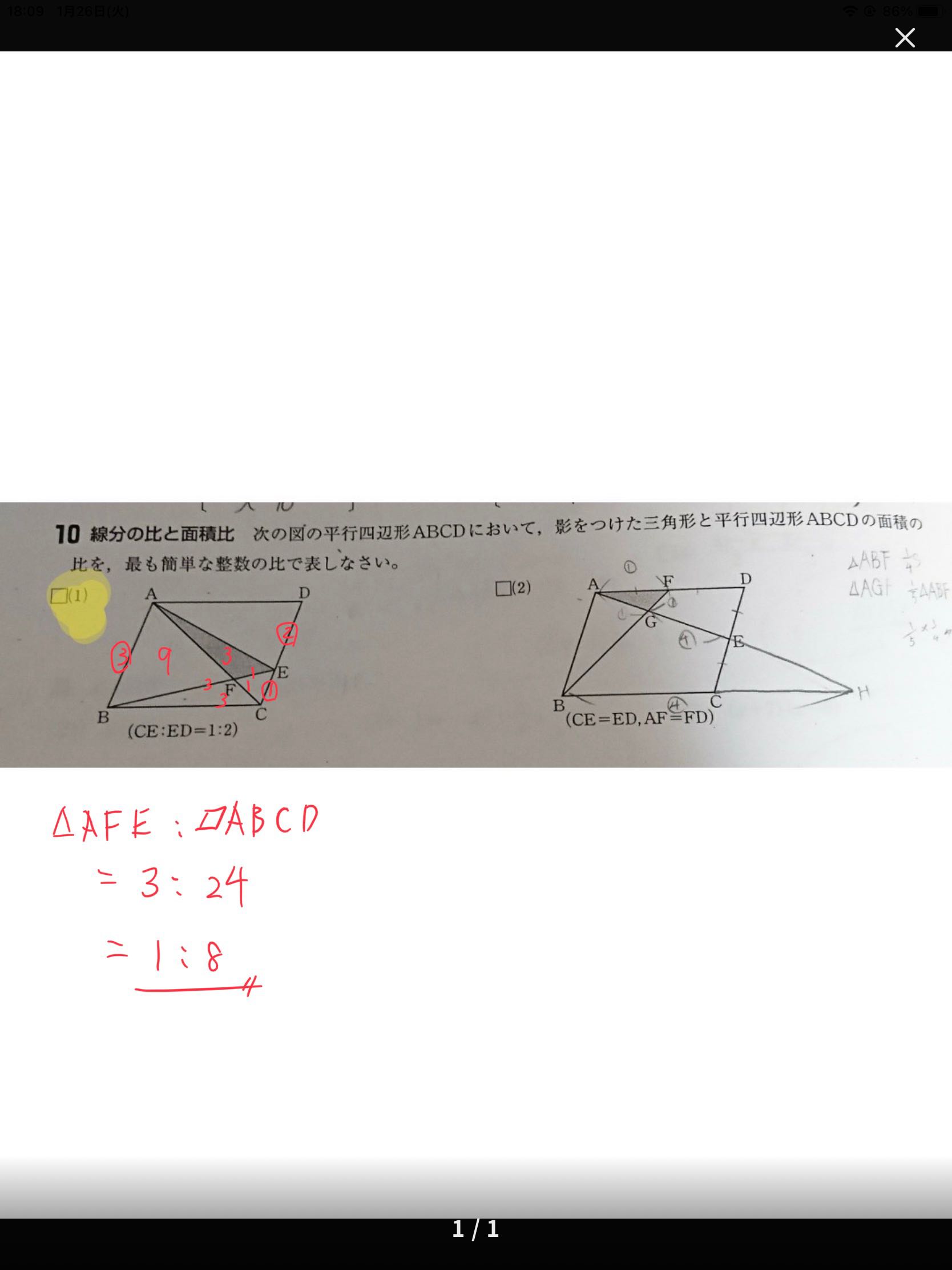



U 10 Abcd Abcd 1right D Descubre Como Resolverlo En Qanda
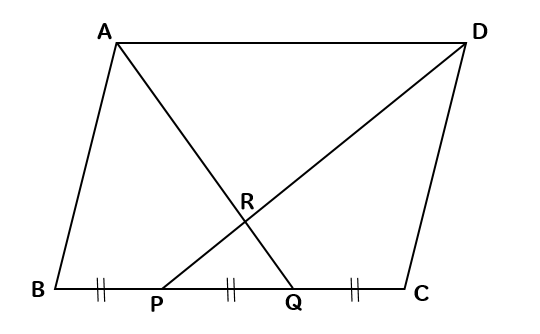



相似 平行四辺形と面積比の問題を徹底解説 数スタ



中3数学 相似や比の応用問題を解くためのテクニック 個別指導塾のyou 学舎日記 公式ブログ



1



0 件のコメント:
コメントを投稿